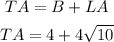1 Answer

Ask a Question

Rosiland · Answer 1 · 2023-06-17T04:42:09+0000

Answer

LA = 4√10

TA = 4 + 4√10

Explanation

To find the Lateral Area (LA) of the pyramid, first, we need to calculate its slant height (s).

Considering the right triangle formed inside the pyramid, we can apply the Pythagorean theorem to find the length of s, as follows:

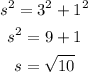
$\begin{gathered} s^2=3^2+1^2 \\ s^2=9+1 \\ s=√(10) \end{gathered}$

Now, we can calculate the lateral area as follows:

$\begin{gathered} LA=(1)/(2)* P\operatorname{*}s \\ \text{ where P is the perimeter of the base of the pyramid. Substituting }P=4*2\text{ and }s=√(10): \\ LA=(1)/(2)\operatorname{*}4\operatorname{*}2\operatorname{*}√(10) \\ LA=4√(10) \end{gathered}$

To find the total area (TA) of the pyramid, first, we need to calculate the area of its base (B). In this case, the base is a square, then its area is:

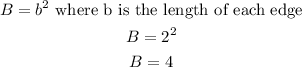
$\begin{gathered} B=b^2\text{ \lparen where b is the length of each edge\rparen} \\ B=2^2 \\ B=4 \end{gathered}$

Finally, the total area is calculated as follows:

$\begin{gathered} TA=B+LA \\ TA=4+4√(10) \end{gathered}$

Click an item in the list or group of pictures at the bottom of the problem and, holding-example-1

0 Comments

Your comment on this question:

Your answer

1 Answer

0 Comments

Your comment on this answer:

Other Questions