Answer:
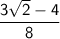
Explanation:
To divide the given expression involving radicals, we can rationalize the denominator. The expression is:
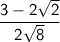
First, simplify the expression in the denominator:
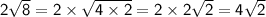
Now, rewrite the expression with the simplified denominator:
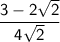
To rationalize the denominator, multiply both the numerator and denominator by the conjugate of the denominator.
The conjugate of
 is
is
 :
:

Now, multiply the numerators and denominators:
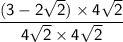
Simplify:
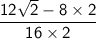
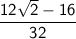
The final simplified expression is:
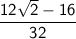
If we want to express this in its simplest form, we can factor out a common factor of 4 from the numerator:
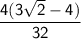
Simplify further by canceling common factors:
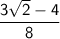
So,
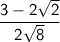 simplifies to
simplifies to
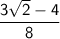 .
.