Question

You earned $135 in simple interest in 8 months at an annual interest rate of 7%. How much

money did you invest? (hint: which variable is missing?)

Answer 1

$2892.86

Explanation:

The formula for simple interest is given by:

`\large\boxed{I=Prt}`

where:

• I is the interest earned.
• P is the principal amount (initial investment).
• r is the annual interest rate (in decimal form).
• t is time (in years).

In this case:

• I = 135
• r = 7% = 0.07
• t = 8 months = 8/12 years

Substitute these values into the formula and solve for P:

`135=P \cdot 0.07 \cdot (8)/(12)`

`135=P \cdot (7)/(100) \cdot (8)/(12)`

`135=P \cdot (56)/(1200)`

`135=(7)/(150)P`

`P=(135 \cdot 150)/(7)`

`P=2892.857142857...`

`P=\$2892.86`

Therefore, the amount of money invested was $2892.86.

Answer 2

$2892.8

Explanation:

Let P be the principal amount invested.

The simple interest earned is calculated using the formula:

`\boxed{\boxed{\sf I = (P* T* R )/(100)}}`

where:

• I is the interest earned
• P is the principal amount invested
• R is the annual interest rate
• T is the time in years

We are given that:

I = $135

R = 7%

T = 8 months = 8/12 years = 2/3 year

Here P is missing variable.

Substituting these values into the formula, we get:

`\sf \$ 135 =(P * (2)/(3) * 7 )/(100)`

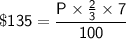
Multiplying both sides by 100, we get:

`\sf \$ 135 * 100 =\frac{P * (2)/(3) * 7 }{\cancel{100}}* \cancel{100}`

`\sf \$ 13500 = P * (2)/(3) * 7`

`\sf \$ 13500 = P * (14)/(3)`

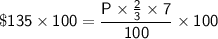
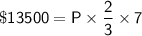
Multiplying both sides by 3/14, we get:

`\sf \$ 13500 * (3)/(14) = P * \cancel{ (14)/(3)}* \cancel{(3)/(14)}`

`\sf \$ 2892.8571428571 = P`

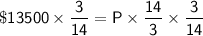
In nearest tenth

`\sf P \approx \$ 2892.8`

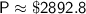
Therefore, we invested $2892.8.