Question

If there are 25 people in a room and 15 chairs, how many different seating arrangements are possible?A)3268760B)7.41x10^11C)4.27x10^18D)4.27x10^19

Answer 1

We will investigate the counting principles that are used for cases of probability evaluation.

There are two possible types of counting principles.

Combinations:

It gives us the total number of possible selections that you can make "given" - " for " something. It is a simple selection process between the subejct and an object. The notation used for determining the number of selections/combinations is expressed as:

`^nC_r`

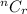
Where,

`\begin{gathered} n\colon\text{ Total number of subjects} \\ r\colon\text{ Total number of ob}\imaginaryJ ects \end{gathered}`

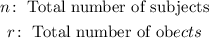
Then we can use the calculator infused functions of " C " combinatorics!

Permutations:

It gives us the total number of possible arrangements comprised of selections and shuffling that you can make "given" - " for " something. It is a simple selection and shuffling process of subject and object. The notation used for determining the number of selections/combinations and re-shuffling is expressed as:

`^nC_r\cdot\text{ r!}`

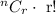
The above means that to determine arrangements we first need to find the number of combinations " C " between the subject and object then we will re-shhuffle the order of each combination paired with an object!

We are given the following:

`\begin{gathered} \text{Subject : people} \\ \text{Object : chairs} \end{gathered}`

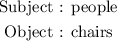
The corresponding variables are:

`\begin{gathered} n\text{ = 25} \\ r\text{ = 15} \end{gathered}`

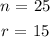
We are to determine the total number of possible arrangements that are possible. Hence, we are looking at the case of permutations that involves the selection and re-shuffle process.

The total number of arrangements can be made as such:

`\begin{gathered} ^(25)C_(15)\cdot15! \\ 4.27\cdot10^(18)\text{ possible arrangements} \end{gathered}`