Answer:
See below
Explanation:
To prove the identity
 , we'll use the sum-to-product trigonometric identity for sine:
, we'll use the sum-to-product trigonometric identity for sine:
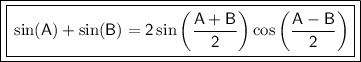
Let
 and
and
 , then substitute into the identity:
, then substitute into the identity:
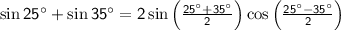
Simplify the expressions inside the sine and cosine functions:
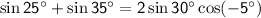
Now, simplify further:
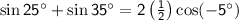
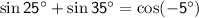
Now, recall that
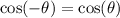
So,
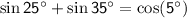
Now, use the fact that
 :
:
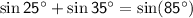
Therefore,
 , and the identity is proved using trigonometric identities.
, and the identity is proved using trigonometric identities.