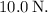the magnitude of the net force on the block while it is sliding is most nearly responses is
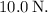
To find the magnitude of the net force on the block while it is sliding down a frictionless inclined plane, we can use the principles of physics, particularly Newton's second law and the concept of gravitational force on an inclined plane. Here's how to approach this problem step by step:
Step 1: Understand the Scenario
- You have a 2 kg block sliding down a frictionless inclined plane.
- The vertical drop is 10 m.
Step 2: Calculate the Gravitational Force Component Along the Incline
- The gravitational force acting on the block is
 where m is the mass and g is the acceleration due to gravity (approximately
where m is the mass and g is the acceleration due to gravity (approximately
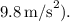
- On an inclined plane, only the component of gravitational force parallel to the plane affects the movement of the block. This component can be found using the sine of the angle of inclination
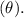
- The angle
 can be determined using trigonometry, since we know the vertical drop and the hypotenuse (the length of the incline):
can be determined using trigonometry, since we know the vertical drop and the hypotenuse (the length of the incline):
![\[ \sin \theta = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{\text{vertical drop}}{\text{length of incline}} \]](https://img.qammunity.org/2024/formulas/physics/high-school/8rvp3c3i89lez0ga5bo1epkw1pfi05cjfm.png)
The force down the incline (parallel component) is given by:
![\[ F_(\parallel) = m * g * \sin \theta \]](https://img.qammunity.org/2024/formulas/physics/high-school/pwd1mxaqlm0gn0f5dl231qzcvivqshpm26.png)
Step 3: Calculate the Force
First, find
![\( \sin \theta \): \[ \sin \theta = \frac{10 \, \text{m}}{20 \, \text{m}} = 0.5 \]](https://img.qammunity.org/2024/formulas/physics/high-school/gj70uxvu5p0m9bpuvo5np6pu88d7qlrlrf.png)
Calculate the gravitational force component along the incline:
![\[ F_(\parallel) = 2 \, \text{kg} * 9.8 \, \text{m/s}^2 * 0.5 \]](https://img.qammunity.org/2024/formulas/physics/high-school/vpmxojr7wup4lg89e05bvb2ms0ol9zw41s.png)
Step 4: Evaluate the Expression
Let's calculate the final value of the force
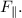
The magnitude of the net force on the block while it is sliding down the inclined plane is approximately
 Therefore, the closest answer among the given options is
Therefore, the closest answer among the given options is