Answer:
13
Explanation:
The velocity is given by:

And the total distance given the velocity is given by:
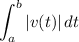
So, the total distance traveled by the particle from t = 1 to t = 6 will be:
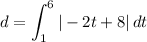
The absolute value tells us that:

So, split the integral into two parts:
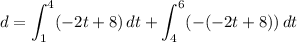
Integrate:
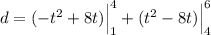
Evaluate:
![\begin{aligned} d&=[(-4^2+8(4))-(-1^2+8)]+[(6^2-8(6))-(4^2-8(4)]\\ &= [16-7]+[-12-(-16)]\\ &=9+4 \\ &=13 \end{aligned}](https://img.qammunity.org/2022/formulas/mathematics/college/f7d5e2ly2exfb8g51npg2b3ttr6irx70ep.png)