Question

Draw a sketch of f(x)= (x+4)^2-5. Plot the point for the vertex, and label the coordinate as a maximum or minimum, and draw & write the equation for the axis of symmetry.

Answer 1

Answer: The vertex is (-4,-5) and the axis of symmetry is x=-4.

Step-by-step explanation:

Given:

f(x)=(x+4)^2-5

The graph for the given equation is:

The point for the vertex is at (-4,-5) and it is also the minimum coordinate.

To find the axis of symmetry, we rewrite first the equation y=(x+4)^2-5 in the form y=ax^2 +bx +c.

So,

`\begin{gathered} y=(x+4)^2-5 \\ y=x^2+8x\text{ +16 -5} \\ y=x^2+8x\text{ +1}1 \end{gathered}`

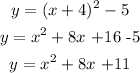
Let:

a=1, b=8, c =11

The formula for the axis of symmetry is:

`x=(-b)/(2a)`

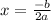
We plug in what we know.

`\begin{gathered} x=(-b)/(2a) \\ =(-8)/(2(1)) \\ =(-8)/(2) \\ x=-4 \end{gathered}`

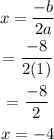
The axis of symmetry is x=-4.

Therefore, the vertex is (-4,-5) and the axis of symmetry is x=-4.