Question

Find the slope of a line that is a) parallel and b) perpendicular to the given line.– 3x – 4y = 1

Answer 1

The line is:

`-3x-4y=1`

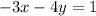
Which is equivalent to:

`\begin{gathered} \Rightarrow4y=-3x-1 \\ \Rightarrow y=-(3x)/(4)-(1)/(4) \end{gathered}`

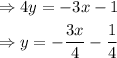
Thus, the slope of the line is equal to -3/4

a) Every line parallel to that one has the same slope, then the answer is -3/4

b) On the other hand, if m_1 and m_2 are the slopes of two perpendicular lines, then:

`m_1\cdot m_2=-1`

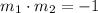
Therefore, since the slope of our line is equal to -3/4, the slope of any line perpendicular to that one is:

`\begin{gathered} m_1\cdot(-(3)/(4))=-1 \\ \Rightarrow m_1=(4)/(3) \end{gathered}`

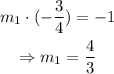
Hence, the answer is 4/3