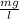This question is incomplete, the complete question is;
A reaction that proceeds by first-order irreversible kinetics is oxidizing chemical A in a wastewater treatment basin with a mean residence time of 1.5 hours. The reaction rate constant is 2.0 Hr-1.The basin is unbaffled and may be characterized as two completely mixed tanks in series. If the steady-state influent concentration is 30 mg/l, find the effluent concentration.
If baffles are placed in the basin so that the basin may be characterized as four completely mixed tanks in series, and the mean residence time remains constant, find the effluent concentration.
Answer:
a) (two completely mixed tanks in series) the find the effluent concentration is 4.8
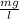
b) (four completely mixed tanks in series) find the effluent concentration is 3.2
Step-by-step explanation:
Given the data in the question;
we can determine the effluent concentration of two completely mixed tanks in series for first order irreversible reaction using the following equation;
C = Co ( 1 / ( 1 + K
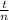 )ⁿ
)ⁿ
t is the mean hydraulic residence time for two completely mixed tanks in series ( 1.5 hr)
Co is initial concentration of the influent ( 30
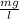 )
)
C is final concentration of effluent,
n is the number of tanks series ( 2)
k is rate constant for the given first order reaction( 2
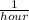 )
)
so we substitute
C = 30
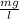 ( 1 / ( 1 + 2
( 1 / ( 1 + 2
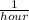 .
.
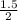 )²
)²
C = 30
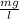 × ( 1/2.5)²
× ( 1/2.5)²
C = 30
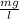 × 0.16
× 0.16
C = 4.8
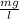
Therefore, (two completely mixed tanks in series) the find the effluent concentration is 4.8
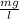
b)
using;
C = Co ( 1 / ( 1 + K
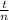 )ⁿ
)ⁿ
t is the mean hydraulic residence time for two completely mixed tanks in series ( 1.5 hr)
Co is initial concentration of the influent ( 30
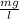 )
)
C is final concentration of effluent,
n is the number of tanks series ( 4)
k is rate constant for the given first order reaction( 2
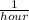 )
)
so we substitute
C = 30
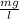 ( 1 / ( 1 + 2
( 1 / ( 1 + 2
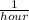 .
.
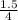 )⁴
)⁴
C = 30
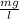 × ( 1/1.75)²
× ( 1/1.75)²
C = 30
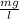 × 0.107
× 0.107
C = 3.2
Therefore, (four completely mixed tanks in series) find the effluent concentration is 3.2