The number of degrees of freedom in a chi-square goodness of fit test equals the k - 1
To determine this
k denotes the number of categories or groups.
This is owing to the fact that the chi-square goodness of fit test compares observed frequencies to expected frequencies in each category, and there is one less predicted frequency than observed frequency due to the limitation that the sum of the frequencies must equal the total number of observations. If there are four categories, there are three anticipated frequencies and four observed frequencies.
The formula for obtaining the chi-square goodness of fit test statistic is as follows:
 =Σ
=Σ
 -
-
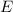
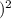 / E]
/ E]
where:
The observed frequency in a category is denoted by O.
The expected frequency in a category is denoted by E.
The greater the chi-square test score, the stronger the evidence that the observed frequencies do not equal the expected frequencies. A crucial value from a chi-square distribution with k - 1 degrees of freedom is used to compare the chi-square test statistic. If the chi-square test statistic is greater than the critical value, the null hypothesis is rejected, and it is inferred that the observed and predicted frequencies are not equal.