Question

What is the variance for the following discrete probability distribution? x p(x) 0 0.36 1 0.1 2 0.03 3 0.14 4 0.37

Answer 1

The variance for the given discrete probability distribution is approximately 3.0

What is the variance for the following discrete probability distribution?

To calculate the variance for a discrete probability distribution, to compute the expected value (mean) and then calculate the squared difference between each value and the mean.

Finally, we multiply the squared differences by their corresponding probabilities and sum them up.

Here's how you can calculate the variance for the given discrete probability distribution:

Step 1: Calculate the expected value (mean)

Expected value (mean) = Σ(x * p(x))

= (0 * 0.36) + (1 * 0.1) + (2 * 0.03) + (3 * 0.14) + (4 * 0.37)

= 0 + 0.1 + 0.06 + 0.42 + 1.48

= 2.06

Step 2: Calculate the squared difference between each value and the mean

`(0 - 2.06)^2 = 4.2436\\(1 - 2.06)^2 = 1.1236\\(2 - 2.06)^2 = 0.0036\\(3 - 2.06)^2 = 0.7396\\(4 - 2.06)^2 = 3.3636`

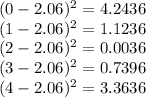
Step 3: Multiply the squared differences by their corresponding probabilities

(0.36 * 4.2436) + (0.1 * 1.1236) + (0.03 * 0.0036) + (0.14 * 0.7396) + (0.37 * 3.3636)

= 1.528496 + 0.11236 + 0.000108 + 0.103344 + 1.243932

= 2.98824
`\approx` 3.0

Therefore, the variance for the given discrete probability distribution is approximately 3.0

What is the variance for the following discrete probability distribution?

x :0, 1, 2, 3, 4

p(x) 0.36, 0.1, 0.03, 0.14, 0.37