Question

Two free charges +q and +4q are a distance l apart. A third charge is placed so that the entire system is in equilibrium. Find the location, magnitude and sign of the third charge.

Answer 1

the value of the charge is q₃ =
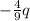`- (4)/(9) q`- 4/9 q, in the position x= l/3

Step-by-step explanation:

The forces in this system are given by Coulomb's law

F =
`k (q_1 q_2)/( r^2)`

As the forces are vector, we must add them as a vector, also let us take that charges of the same sign repel and charges of the opposite sign attract, therefore for the system to be in equilibrium the third charge must be of the opposite sign, that is, NEGATIVE .

Let's analyze the situation for card charge, let's use the indexes 1 for the charge q₁ = + q located at the origin (x₁ = 0), index 2 for the face q₂ = + 4q located at x₂ = l and the index 3 for the third charge

Let's find the location of charge 3 so that it is in balance

∑ F = F₁₃ - F₂₃ = 0

F₁₃ = F₂₃

we seek every force

F₁₃ = k
`(q_1q_3 )/(x_(13)^2)`

F₂₃ = k
`(q_2q_3)/( x_(23)^2)`

the distances are

x₁₃ = x-0 = x

x₂₃ = l -x

we substitute

k \frac{q_1q_3 }{x^2} = k \frac{q_2q_3 }{(l-x)^2}

we solve

(l-x)² =
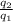`(q_2)/(q_1)` x²

l² - 2lx + x² = \frac{4q}{q} x²

3x² + 2l x - l² = 0

we solve the quadratic equation

x = [-2l ±
`√(4l^2 + 4\ 3\ l^2)` / (2 3)

x = [-2l + 2l
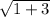`√(1+3)`] / 6 = 2l [-1 ± 2] / 6

x₁ = -l

x₂ = l / 3

as charge 3 must be between the two charges the correct answer is

x = l / 3

with charge 3 in this location it remains in equilibrium regardless of the value of its NEGATIVE charge.

now let's analyze the force on the other charges

charge 1 so that it is in balance

∑F = F₁₃ - F₁₂ = 0

F₁₃ = F₁₂

`k (q_1q_3)/((l/3)^2) = k (q_1 q_2)/( l^2)`

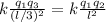
l² q₃ = q₂ (l/3)²

q₃ = q₂ / 9

q₃ = 4q / 9

q₃ =
`(4)/(9) q`

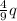
in summary the value of the charge is q₃ =
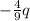`- (4)/(9) q`- 4/9 q

in the position x= l/3