Question

3. A rescue helicopter is lifting a person (weight = 822 N) from a capsized boat by means of

a cable and harness.

(a) Draw a free-body diagram of the person. Label all the forces exerted on the person
with appropriate labels.

(b) What is the tension in the cable when the person is given an upward acceleration of 1.10 m/s^2? You can neglect the mass of the harness.

Answer 1

a. Refer to explanation below and the attached image

b. 915 N

Step-by-step explanation:

Let's address this physics problem by first understanding the scenario and then proceeding to solve each part methodically.

For part (a), the free-body diagram (FBD) is a simple yet powerful tool that illustrates all the forces acting on an object. In this case, the object is the person being lifted. The FBD helps us understand the influences on the person without the complexities of their environment. I will draw this for you with labels for gravitational force and tension.

For part (b), to find the tension in the cable, we'll use Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration (F_net=ma). The net force in this scenario is the tension in the cable minus the weight of the person. Since we're given the weight and the upward acceleration, we can rearrange the equation to solve for the tension in the cable.

Now, let's solve each part step-by-step.

`\hrulefill`Part (a): Free-Body Diagram
`\hrulefill`

The forces acting on the person are listed below:

• Weight (w): This force acts downward and is equal to the gravitational force exerted on the person by the Earth.

• Tension (T): This force acts upward and is provided by the cable pulling the person.

Attached in the image is the free-body diagram for part (a). This shows the forces acting on the person: the downward gravitational force (weight) of 822 N, and the upward tension force (T) exerted by the cable from the helicopter.

`\hrulefill`Part (b): Calculating the Tension
`\hrulefill`

Now, let's calculate the tension in the cable. We are given:

• The weight of the person, w = 822 N
• The upward acceleration, a = 1.10 m/s²

We know that weight 'w' is the gravitational force, which is w = mg, where 'g' is the acceleration due to gravity (g = 9.8 m/s²). Therefore, we can find the mass 'm' of the person as:

`\Longrightarrow m= (\vec w)/(g)`

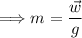
Once we have the mass, we can use Newton's second law to find the tension 'T' when the person is accelerating upwards:

`\Longrightarrow \sum \vec F_y: \vec T - \vec w=m \vec a`

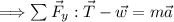
Rearranging for 'T':

`\Longrightarrow \vec T = m \vec a + \vec w\\\\\\\\\Longrightarrow \vec T = m \vec a + mg\\\\\\\\\therefore \vec T = m(\vec a + g)`

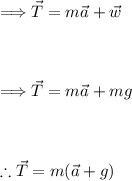
Let's perform the calculations to find the mass of the person and the tension in the cable.

The mass of the person:

`\Longrightarrow m= (822 \ N)/(9.8 \ m/s^2)\\\\\\\\\therefore m \approx 83.9 \ kg`

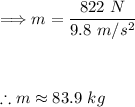
Now finding the tension in the cable:

`\Longrightarrow \therefore \vec T = (83.9 \ kg)(1.10 \ m/s^2 + 9.8 \ m/s^2)\\\\\\\\\Longrightarrow \therefore \vec T = (83.9 \ kg)(10.9 \ m/s^2)\\\\\\\\\therefore \boxed{\vec T \approx 915 \ N}`

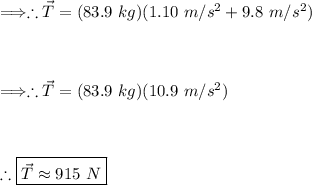
Thus, the tension in the cable is approximately 915 N.