Question

2. A space traveler weighs 580 N on Earth where the gravitational field strength is 9.8

N/kg. What will the traveler weigh on another planet where the gravitational field
strength is 15.7 N/kg?


3. A rescue helicopter is lifting a person (weight = 822 N) from a capsized boat by means of
a cable and harness.

(a) Draw a free-body diagram of the person. Label all the forces exerted on the person
with appropriate labels.

Answer 1

2) Weight = 929.13 N

Step-by-step explanation:

Part 2:

To solve this question, we can use the following equation:

`\boxed{\boxed{\sf Weight = Mass * \textsf{Gravitational Field Strength}}}`

We know the weight of the traveler on Earth, as well as the gravitational field strength on Earth. We want to find the weight of the traveler on another planet, where the gravitational field strength is 15.7 N/kg.

First, we need to find the mass of the traveler. We can do this by dividing the weight of the traveler on Earth by the gravitational field strength on Earth:

`\sf Mass =\frac{ Weight }{\textsf{ Gravitational Field Strength}}`

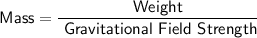
Substitute the known value:

`\sf Mass =( 580 N )/(9.8 N/kg)`

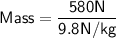
Mass = 59.183673469387 kg

Mass = 59.18 kg ( in 4 d.p.)

Now that we know the mass of the traveler, we can find the weight of the traveler on another planet by multiplying the mass of the traveler by the gravitational field strength on the other planet:

`\sf Weight = Mass * \textsf{Gravitational Field Strength}`

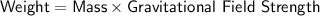
Substitute the known value:

`\sf weight = 59.18 * 15.7 N/kg`

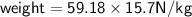
Weight = 929.126 N

Weight = 929.13 N ( in 2 d.p)

Therefore, the traveler will weigh 929.13 N on the other planet.

`\hrulefill`

Part 2:

Free-body diagram of the person:

____

___|___________|

|______|. |

|. Tension(Upward force)

|

|

_o_

| 822 N( weight) downward force)

^

The forces exerted on the person are:

Weight: This is the force of gravity acting on the person. It is directed downwards.

Tension: This is the force exerted on the person by the cable and harness. It is directed upwards.

The person is in equilibrium, which means that the net force acting on the person is zero. This means that the tension in the cable and harness must be equal to the weight of the person.

Therefore, the free-body diagram of the person will look like the diagram above, with the weight and tension forces labeled.

Answer 2

≈ 930 N

Step-by-step explanation:

To solve this problem, we can use the concept of weight as the product of mass and gravitational field strength. The traveler's weight on Earth is given, and using the gravitational field strength on Earth, we can calculate their mass. Then we can find out what this mass would weigh on another planet by multiplying it by the gravitational field strength of the other planet.

Given:

• w = 580 N
• g_E = 9.8 N/kg
• g_op = 15.7 N/kg

Now lets solve.

`\hrulefill`

First, let's calculate the mass of the traveler using the weight on Earth:

`\Longrightarrow \vec w_E=mg_E\\\\\\\\\therefore m = (\vec w _ E)/(g_e)`

Plugging in our values:

`\Longrightarrow m = (580 \ N)/(9.8 \ N/kg)\\\\\\\\\therefore m \approx 59 \ kg`

Once we have the mass, we can then calculate the weight on the other planet by using the gravitational field strength of the other planet:

`\Longrightarrow \vec w_(op)=mg_(op)\\\\\\\\\Longrightarrow \vec w_(op)=(59 \ kg)(15.7 \ N/kg)\\\\\\\\\therefore \boxed{\vec w_(op) \approx 930 \ N}`

The mass of the space traveler is approximately 59.18 kg. On another planet where the gravitational field strength is 15.7 N/kg, the traveler would weigh approximately 930 N.