Question

Mr. Frey is riding his Motorcycle on a flat street and a squirrel jumps out in front of him. He slams on the brakes causing 2,419N of frictional force. What is mew between the tires and the road?

Mr. Frey is 90kg

The motorcycle 200kg

Use 9.8 for acceleration of gravity

Answer 1

μ ≈ 0.8512

Step-by-step explanation:

To solve for the coefficient of friction (often denoted as μ) between the tires and the road, we use the relationship between frictional force (f), normal force (n), and μ, which is given by the equation:

`\vec f_k=\mu _k\vec n`

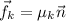
The normal force, in this case, is the force exerted by the road to support the weight of Mr. Frey and his motorcycle, and it is equal to the combined weight of Mr. Frey and the motorcycle times the acceleration due to gravity. Hence, the normal force is:

`\vec n = \vec w= (m_{\text{Mr. Frey}}+m_{\text{Motorcycle}})g\\\\\\\\\Longrightarrow \vec n = (90 \ kg + 200 \ kg)(9.8 \ m/s^2)\\\\\\\\\Longrightarrow \vec n = (290 \ kg) (9.8 \ m/s^2)\\\\\\\\\therefore \vec n = 2842 \ N`

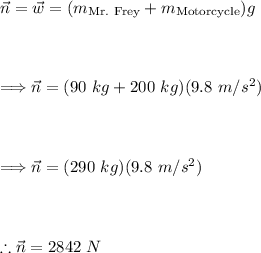
Rearranging our friction equation we can solve for the coefficient of friction by plugging in what we know:

`\vec f_k=\mu _k\vec n \rightarrow \mu_k = (\vec f_k)/(\vec n) \\\\\\\\\Longrightarrow \mu_k = (2419 \ N)/(2842 \ N)\\\\\\\\\therefore \boxed{\mu _k \approx 0.8512}`

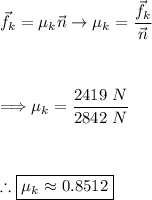
Thus, μ ≈ 0.8512.