Answer:
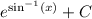
Explanation:
To solve this integral, we will consider the properties of the inverse sine function and its relation to the expression √(1 - x²) in the denominator, which is reminiscent of the derivative of the inverse sine function. By recognizing this relationship, we can find the integral of the given function.
Given integral:


Using u-substitution, let u = sin⁻¹(x) then du = 1/√(1-x²) · dx. Make these substitutions:
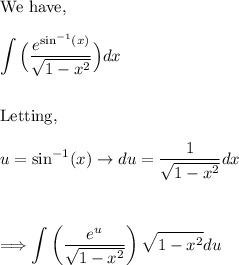
With these substitutions, our integral becomes:
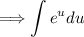
Which is straightforward to integrate. Let's perform the computation. The integral of e^u with respect to u is simply e^u:
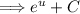
Now, we need to substitute back using u = sin⁻¹(x) to express our result in terms of 'x'.
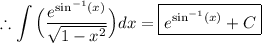
Thus, the integral is solved where 'C' is the constant of integration.