Question

The area of a triangle is 2312 . Two of the side lengths are 93 and 96 and the included angle is obtuse. Find the measure of the included angle, to the nearest tenth of a degree.

Answer 1

to facilitate the exercise we will draw the triangle

We start using the area

`A=(b* h)/(2)`

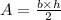
where A is the area, b the base and h the height

if we replace A=2312 and b=96 we can calculate the height(h)

`\begin{gathered} 2312=(96* h)/(2) \\ \\ h=(2312*2)/(96) \\ \\ h=(289)/(6) \end{gathered}`

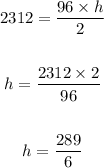
now to calculate the measure of the angles we can solve the red triangle

first we find Y using trigonometric ratio of the sine

`\sin (\alpha)=(O)/(H)`

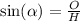
where alpha is the reference angle, O the opposite side from the angle and H the hypotenuse of the triangle

using Y like reference angle and replacing

`\sin (y)=((289)/(6))/(93)`

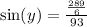
simplify

`\sin (y)=(289)/(558)`

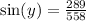
and solve for y

`\begin{gathered} y=\sin ^(-1)((289)/(558)) \\ \\ y=31.2 \end{gathered}`

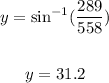
value of angle y is 31.2°

Y and X are complementary because make a right line then if we add both numbers the solution is 180°

`\begin{gathered} y+x=180 \\ 31.2+x=180 \end{gathered}`

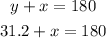
and solve for x

`\begin{gathered} x=180-31.2 \\ x=148.8 \end{gathered}`

measure of the included angle is 148.8°