Question

A 1.0 C charged object and a 2.0 C charged object are separated by 100 m. Where should a -1.0x10-3 C charged object be placed on a line between the positively charged objects so that the net electrical force exerted on the negatively charged object is zero

Answer 1

x = 41.2 m

Step-by-step explanation:

The electric force is a vector magnitude, so it must be added as vectors, remember that the force for charges of the same sign is repulsive and for charges of different sign it is negative.

In this case the fixed charges (q₁ and q₂) are positive and separated by a distance (d = 100m), the charge (q₃ = -1.0 10⁻³ C)) is negative so the forces are attractive, such as loads q₃ must be placed between the other two forces subtract

F = F₁₃ - F₂₃

let's write the expression for each force, let's set a reference frame on the charge q1

F₁₃ =
`k (q_1 q_3)/(x^2)`

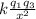
F₂₃ =
`k (q_2 q_3)/((d-x)^2)`

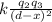
they ask us that the net force be zero

F = 0

0 = F₁₃ - F₂₃

F₁₃ = F₂₃

k \frac{q_1 q_3}{x^2} =k \frac{q_2 q_3}{(d-x)^2}

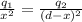`(q_1)/(x^2) = (q_2)/((d-x)^2 )`q1 / x2 = q2 / (d-x) 2

(d-x)² =
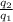`(q_2)/(q_1)` x²

we substitute

(100 - x)² = 2/1 x²

100- x = √2 x

100 = 2.41 x

x = 41.2 m