Question

Solve: logg x + logg (x + 6) = logg (5x+12)

Answer 1

x = 3

Explanation:

We can solve for x using the following steps:

Step 1: Apply the product rule of logs:

• Note that all three logs are common logs, whose base is 10 (the 10 simply isn't written, since it's implied).

The product rule of logs says that the log of a products equals the sum of the logs:

Example using a as the base and m and n as the arguments of the logs:

`log_(a)(xy)=log_(a)x + log_(a)y`

Since x and (x + 6) are the arguments on the left-hand side, we can combine them into a single log by applying the product rule:

log (x(x + 6) = log (5x + 12)

log (x^2 + 6x) = log (5x + 12)

Step 2: Apply the logarithmic identity to solve for x using the arguments directly:

• The logarithmic identity says that when you have a log with the same base and different arguments on two sides of an equation, the arguments are equal to each other.

Example using a as the base and x and y as the arguments:

`log_(a)x=log_(a)y\\ x=y`

Because we have the same base for both logs (i.e., 10), we can solve with the arguments directly:

x^2 + 6x = 5x + 12

Step 3: Put the quadratic in standard form:

The general equation of the standard form of a quadratic equation is given by:

ax^2 + bx + c = 0, where:

• a, b, and c are constants.

• Setting the quadratic in this form will allow us to solve using the quadratic equation.

Thus, we can set the quadratic in standard form by subtracting 5x and 12:

(x^2 + 6x = 5x + 12) - 5x - 12

x^2 + x - 12 = 0

For x^2 + x - 12:

• a = 1,
• b = 1,
• and c = -12.

Quadratic equation:

The quadratic equation is given by:

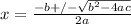`x=(-b+/-√(b^2-4ac) )/(2a)`, where:

• x is (are) the solution(s) to the quadratic,
• and a, b, and c are the same constants form the standard form.

Thus, we can solve the quadratic by substituting 1 for a, 1 for b, and -12 for c in the quadratic equation:

`x=(-1+/-√(1^2-4(1)(-12)) )/(2(1))\\ \\x=(-1+/-√(49) )/(2)`

Now, we can determine the positive solution and the negative solution to the quadratic:

Positive solution:

`x=(-1+/-√(49) )/(2)\\\\x=-(1)/(2)+(√(49) )/(2)\\ \\ x=-(1)/(2)+(7)/(2)\\ \\ x=(6)/(2) \\ \\x=3`

Thus, one of the solutions to the quadratic is 3.

Negative solution:

`x=(-1+/-√(49) )/(2)\\\\x=-(1)/(2)-(√(49) )/(2)\\ \\ x=-(1)/(2)-(7)/(2)\\ \\ x=-(8)/(2) \\ \\x=-4`

Thus, the other solution to the quadratic is -4.

Step 4: Determine which solution is correct for x:

We cannot have a negative argument in a logarithm since you can't can never get a negative number when raising a base to an exponent.

Therefore, x = 3 is the correct solution.

----------------------------------------------------------------------------------------------------------

Optional Step 5: Check the validity of the answer:

We can check that our answer is correct by substituting 3 for x and seeing if we get the same answer on both sides of the equation:

log (3) + log (3 + 6) = log (5(3) + 12)

log (3(3 + 6)) = log (15 + 12)

log (3(9)) = log (27)

log (27) = log (27)

Therefore, our answer for x is correct.