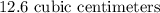Question

How do i find the volume to the nearest 1 decimal place?

Answer 1

The volume of a cylinder is expressed as

`\begin{gathered} V=\pi* r^2* h \\ where \\ V\Rightarrow volume\text{ of the cylinder} \\ r\Rightarrow radius\text{ of its circular ends} \\ h\Rightarrow height\text{ of the cylinder} \end{gathered}`

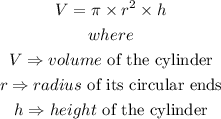
Given the cylinder below:

we have

`\begin{gathered} height\text{ of the cylinder = 4 cm} \\ diameter\text{ of the circular end = 2 cm} \end{gathered}`

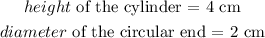
but

`\begin{gathered} radius=(diameter)/(2) \\ \Rightarrow r=(d)/(2)=(2cm)/(2)=1\text{ cm} \end{gathered}`

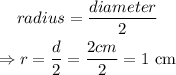
Thus, the volume of the cylinder is evaluated by substituting the values of 4 cm and 1 cm for h and r respectively into the volume formula.

`\begin{gathered} V=\pi*1cm*1cm*4cm \\ =12.56637 \\ \approx12.6\text{ cubic centimeters} \end{gathered}`

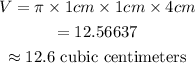
Hence, the volume of the cylinder, to the nearest 1 decimal place is

`12.6\text{ cubic centimeters}`