Question

(ITA-1985) Be f: IR ⇒ IR a function satisfying f(x+∝y) = f(x) + ∝f(y) for all ∝,x,y ∈ IR. If (
`(a_(1) ,a_(2),a_(3),...,a_(n) )`) is an arithmetric progression of ratio d, then we can say that
`(f(a_(1)) ,f(a_(2)),f(a_(3)),...,f(a_(n) ))`

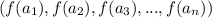
a) It is an arithmetric progression of ratio d.
b) It is an arithmetric progression of ratio f(d) whose first term is
`a_(1)`.
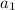
c) It is a geometric progression of ratio f(d).
d) It is an arithmetric progression of ratio f(d).
e) Nothing can be said.

Answer 1

Answer: letter D

Explanation:

Resolusion below