Question

the scatter plot shows the number of years of experience, x, and the hourly pay rate,y, for each of 25 cashier im California. (a) write an approximate equation of the line of best fit for the data. It doesn't have to be the exact line of best fif. (b) using your equation from part (a), predict the hourly pay rate for a cashier with 14 years of experience. Note that you can use the graphing tools to help you approximate the line. (a) write an approximate equation of the line of best fit .y=(b) using your equation from part (a), predict the hourly pay rate for a cashier with 14 years of experience. $=

Answer 1

Input data

Points

(2, 8)

(20, 18)

First of all, remember what the equation of a line is:

y = mx+b

Where:

m is the slope, and

b is the y-intercept

First, let's find what m is, the slope of the line...

`\begin{gathered} m=(y2-y1)/(x2-x1) \\ m=(18-8)/(20-2) \\ m=(5)/(9) \end{gathered}`
`\begin{gathered} b=y-mx \\ b=8-(5)/(9)2 \\ b=(62)/(9) \end{gathered}`

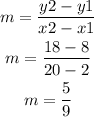
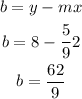
The equation of the line that passes through the points. For this case we can use the linear model given:

`y=0.55x+6.8`

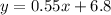
predict the hourly pay rate for a cashier with 14

`\begin{gathered} y=0.55(14)+6.8 \\ y=14.5\text{ dollars per hour} \end{gathered}`

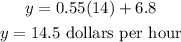
(a) y = 0.55x+6.8

(b) 14.5 dollars per hour