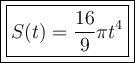Question

Help me please it’s in the picture

Answer 1

`S(t) =(16)/(9)\pi t^4`

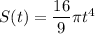
Explanation:

The surface area (S) in square meters of a hot-air balloon is given by

`S(r) = 4\pi r^2`

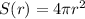
where r is the radius of the balloon (in meters).

The radius (r) is increasing with time (t) in seconds according to the formula:

`r(t) = (2)/(3)t^2, \quad t\geq 0`

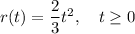
To find the surface area (S) of the balloon as a function of time (t), we can simply substitute the expression for the radius r(t) into the formula for S(r):

`S(t) = 4\pi \left((2)/(3)t^2\right)^2`

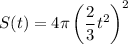
Now, simplify this expression:

`S(t) = 4\pi \cdot(2^2)/(3^2)(t^2)^2`

`S(t) = 4\pi \cdot (4)/(9)t^4`

`S(t) =(16)/(9)\pi t^4`

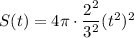
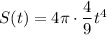
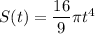
So, the surface area (S) of the hot-air balloon as a function of time (t) is:

`\large\boxed{\boxed{S(t) =(16)/(9)\pi t^4}}`