Question

List all possible rational zeros for the function. (Enter your answers as a comma-separated list.)f(x) = 2x3 + 3x2 − 8x + 5

Answer 1

We will list all the possible rational zeros for the polynomial

`f(x)=2x^3+3x^2-8x+5`

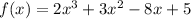
to find it we will apply the Rational root theorem. It states that each rational zero(s) of a polynomial with integers coefficients is of the form

`(p)/(q)`

where:

* p is a factor of the coefficient of the zero order term in the polynomial ( in our case this coefficient is 5)

* q is a factor of the leading coefficient , that is the coefficient that multiply the variable to the biggest power (in our case that coefficient is 2)

* p and q are relative primes, that is , they does not have common factors.

Finding the possibilities for rational roots:

Just summarizing the information until now, we have:

`p=5\text{ and q=2}`

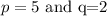
we also have that:

`factors\text{ of 5= \textbraceleft1,5,-1,-5\textbraceright}`

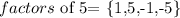
and

`factors\text{ of 2 = \textbraceleft1,-1,2,-2\textbraceright}`

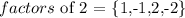
So, on the right of the equations above, we have all the possible values that can take p and q, respectively. It only rests to construct all the possibilities, we do