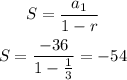Question

Given the pattern -36, 12, -4, ...(a) Write an explicit formula for the pattern.(b) Write a recursive formula for the pattern.(c) Does the pattern converge or diverge? If it converges, to what value does it converge?(d) If you added the terms in this pattern, would the sum converge or diverge? If it converges, to what value does it converge?

Answer 1

`\begin{gathered} a)a_n=-36\cdot(1)/(3)^(n-1) \\ b)\text{ }a_n=(1)/(3)\cdot a_(n-1) \\ c)\text{ converges to -54} \\ d)\text{ s=-54} \end{gathered}`

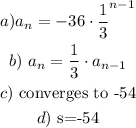
Explanation:

The explicit and recursive formula for a geometric sequence is represented by the following:

`\begin{gathered} \text{ Explicit formula:} \\ a_n=a_1\cdot r^(n-1) \\ \text{ Recursive formula:} \\ a_n=r\cdot a_(n-1) \\ \text{where,} \\ r=\text{ common ratio} \end{gathered}`

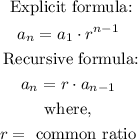
The common ratio of the pattern is:

`\begin{gathered} (-12)/(-36)=(1)/(3) \\ (-4)/(-12)=(1)/(3) \end{gathered}`

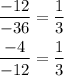
Then, for the explicit formula:

`a_n=-36\cdot(1)/(3)^(n-1)`

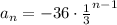
Recursive formula:

`a_n=(1)/(3)\cdot a_(n-1)`

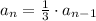
Now, to determine if the pattern converge or diverge:

`\begin{gathered} \lvert r\rvert<1,\text{ the series converge to }(a_1)/(1-r) \\ \lvert r\rvert\ge1,\text{ the series diverges} \end{gathered}`

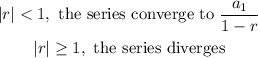
Since the common ratio is less than 1, the series converges to:

`\text{converges to }(-36)/(1-(1)/(3))=-54`

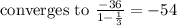
A sum of an infinite geometric series can be determined if it converges since this pattern converges, the sum would converge to;

`\begin{gathered} S=(a_1)/(1-r) \\ S=(-36)/(1-(1)/(3))=-54 \end{gathered}`