Question

10. A farmer is creating a small rectangular pen for her chickens. She has 20 feet of fencing

to build the pen and wants the pen to have an area of at least 16 ft². What are the lengths of fence
she can use to create her desired pen?

a.) 16 ≤l≤ 20
c. 2≤1≤8
b.l≤ 16 or 1 ≥ 20 4
d. 1 ≤2 or 1 ≥ 8
A. 16ft ²

Answer 1

c.) 2≤ l ≤8

Explanation:

The perimeter of the rectangular pen is given by the sum of all four sides, which is twice the length plus twice the width. Since the farmer has 20 feet of fencing, the perimeter (PP) is given by:P=2l+2wP=2l+2wShe wants the pen to have an area (AA) of at least 16 ft², and the area of a rectangle is given by the product of its length and width:A=lwA=lwNow, let's set up the conditions based on the information given:The farmer has 20 feet of fencing, so the perimeter is limited by 2l+2w≤202l+2w≤20.She wants the pen to have an area of at least 16 ft², so lw≥16lw≥16.Now, let's analyze the answer choices:a.) 16≤l≤2016≤l≤20This doesn't consider the width (ww) and doesn't guarantee that the perimeter is within the limit.b.) l≤16l≤16 or l≥20l≥20This doesn't guarantee that the perimeter is within the limit, and it restricts the length to be less than or equal to 16 or greater than or equal to 20.c.) 2≤l≤82≤l≤8This is a reasonable range for the length, but we need to consider the width as well.d.) 1≤l≤21≤l≤2 or 1≥81≥8This also doesn't guarantee that the perimeter is within the limit, and it doesn't make logical sense to have a width greater than or equal to 8.

Answer 2

c. 2 ≤ l ≤ 8

Explanation:

To solve this problem, we can use the following steps:

Set up two equations.

Let the length of the pen be l and the width of the pen be w.

We know that the perimeter of the pen is 20 feet, so we can write the following equation:

`\sf 2l + 2w = 20` ……[i]

We also know that the area of the pen must be at least 16 square feet, so we can write the following equation:

`\sf lw ≥ 16`

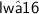
Solve the first equation for l.

Subtracting 2w from both sides of the equation, we get.

`\sf 2l + 2w - 2w = 20-2w`

`\sf 2l = 20 - 2w`

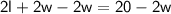
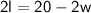
Dividing both sides of the equation by 2, we get:

`\sf (2l )/(2)=( 20 - 2w)/(2)`

`\sf l = 10 - w`

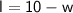
Substitute the expression for l into the second equation. Substituting 10 - w for l in the second equation, we get:

`\sf (10 - w)w ≥ 16`

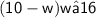
Solve the second equation.

Expanding the left-hand side of the equation, we get:

`\sf 10w - w^2 ≥ 16`

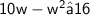
Subtracting 16 from both sides of the equation, we get:

`\sf w^2 - 10w + 16 ≤ 0`

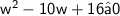
This equation can be factored as follows:

`\sf w^2 - (8+2)w + 16 ≤ 0`

`\sf w^2 -8w - 2w + 16 ≤ 0`

`\sf w(w-8)-2(w-8) ≤ 0`

`\sf (w - 8)(w - 2) ≤ 0`

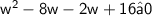
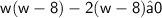
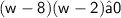
This means that w must be between 2 and 8 inclusive.

Substitute the possible values of w into the expression for l. If w = 2, then l = 10 - 2 = 8.

If w = 8, then l = 10 - 8 = 2.

Therefore, the lengths of fence the farmer can use to create her desired pen are 8 feet and 2 feet.

So, the answer is c. 2 ≤ l ≤ 8