Question

Part F: Write the equation of the line given
(3,-2) (1,2)
y

Answer 1

y = -2x + 4

Explanation:

Pre-Solving

We are given that a line passes through (3, -2) and (1,2).

We want to write the equation of this line.

There are 3 ways to write the equation of the line.

• Slope-intercept form, which is y=mx+b where m is the slope and b is the y-intercept.
• Standard form, which is ax+by=c, where a, b, and c are free integer coefficients but a and b cannot be 0.
• Point-slope form, which is
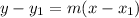  `y-y_1=m(x-x_1)` where m is the slope and
  `(x_1,y_1)` is a point.

As the question doesn't specify, we can use any one of the forms. However, let's write the equation in slope-intercept form, as that is the most common way.

Solving

Slope

First, we need to find the slope of the line.

The slope (m) can be found using the formula
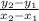`(y_2-y_1)/(x_2-x_1)`, where
`(x_1,y_1)` and
`(x_2,y_2)` are points.

We can label the values of the points prior to calculating.

We get:

`x_1=3\\y_1=-2\\x_2=1\\y_2=2`

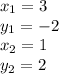
Now, substitute into the formula.

`m=(y_2-y_1)/(x_2-x_1)`

`m=(2--2)/(1-3)`

`m=(2+2)/(1-3)`

`m=(4)/(-2)`

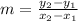
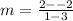
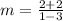
m = -2

The slope is -2.

Y-intercept

We can substitute -2 as m in y=mx+b.

y = -2x + b

Now, we need to find b.

As the equation passes through (3,-2) and (1,2), we can use either one of them to help solve for b.

Taking (3, -2) for instance:

Substitute 3 as x and -2 as y.

-2 = -2(3) + b

Multiply.

-2 = -6 + b

Add 6 to both sides.

4 = b

Substitute into the equation.

Our line is y = -2x + 4