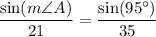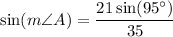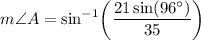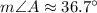Question

PLEASE HELP IM STRUGGLING I GOT SICK AND I NEED TO FINISH THIS BY LIKE TOMORROW

B
3y+20
3x+9
E
95⁰
AAFC AEBD
36⁰
49"
7x
na
8x-6
77
D
Use the congruency stateplants to find each valus.
X
BE
GF
ΜΖΑ
DE
MZD
N =
mZK
MZJ
MZH
GK
HL
ATHLAKGJ
3a+21,
H
K
(42)
3a
5a-7
J

Answer 1

x = 3

y = 5

a = 14

z = 8

AC = ED = 15

BE = FA = 35

CF = DB = 21

`m\angle H = m\angle L = m\angle G = m\angle J = 74\°`

`m\angle F = m\angle B = 36\°`

`m\angle A = m\angle E = 49\°`

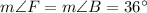
Explanation:

First, we have to recognize that dimension of congruent shapes are equal. We are given the congruency statements:

• 
  `\triangle AFC \cong \triangle EBD`
• 
  `\triangle THL \cong \triangle KGJ`

From these statements, we can equate certain side lengths:

• 
  `AC = ED`
• 
  `BE=FA`
• 
  `IH = KG`

We can also identify through the Isosceles Triangle Theorem that:

• 
  `KG = JK`

because
`\triangle THL` and
`\triangle KGJ` have congruent base angles and are therefore isosceles triangles.

Hence, we can also declare that:

• 
  `IH = JK`

by the transitive property of equality.

Next, we can plug in the labeled values for these side lengths and solve for the variables:

`\begin{aligned}AC &= ED\\ 3x+9 &= 8x-6 \\ 9 &= 5x - 6 \\ 15 &= 5x \\ 3 &= x\end{aligned}`

⇒
`\boxed{x=3}`

`\begin{aligned}AC = ED &= 3x + 9 \\ &= 3(3) + 9\\ &= 9+9 \\ &= 18\end{aligned}`

`\begin{aligned}CF = DB &= 7x \\ &= 7(3) \\ &= 21\end{aligned}`

____________

`\begin{aligned}BE &= FA\\ 3y+20 &= 7y \\ 20 &= 4y \\ 5 &= y\end{aligned}`

⇒
`\boxed{y=5}`

`\begin{aligned}BE = FA &= 7y \\ &=7(5) \\ &= 35\end{aligned}`

____________

`\begin{aligned}IH &= JK\\ 3a+21&=5a-7 \\ 21&= 2a-7 \\ 28 &= 2a \\ 14 &= a\end{aligned}`

⇒
`\boxed{a=14}`

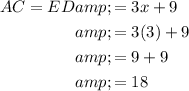
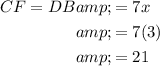
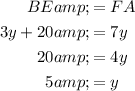
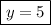
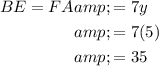
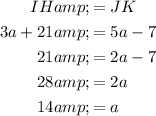
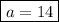
Next, we can solve for z using the fact that CPCTC (Corresponding Parts of Corresponding Triangles are Congruent):

`4z = 32`

`\boxed{z=8}`

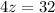
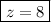
Finally, we can solve for the isosceles triangles' angle measures using our knowledge that the interior angles of a triangle add to 180°F.

(I will call the isosceles triangles' base angles
`b`)

`\begin{aligned}32 + 2b &= 180\\ 2b&=148\\b&=74\end{aligned}`

⇒
`\boxed{m\angle H = m\angle L = m\angle G = m\angle J = 74\°}`

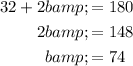
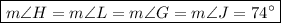
And we can solve for the rest of the angles using CPCTC:

`m\angle F = m\angle B = 36\°`

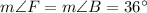
Thus,

`95 + 36 + m\angle A = 180`

`m\angle A = 49\° = m\angle E`

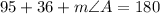
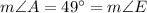
Further Note

When solving for the angle measures using the Law of Sines, we can see that the given side lengths do not match the angles. For example:

`(\sin(m\angle A))/(21) = (\sin(95\°))/(35)`

`\sin(m\angle A) = (21\sin(95\°))/(35)`

`m\angle A = \sin^(-1)\!\left((21\sin(96\°))/(35)\right)`

`m\angle A \approx 36.7\°`