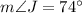Question

P

PLEASE HELP IM STRUGGLING I GOT SICK AND I NEED TO FINISH THIS BY LIKE TOMORROW



B
3y+20
3x+9
E
95⁰
AAFC AEBD
36⁰
49"
7x
na
8x-6
77
D
Use the congruency stateplants to find each valus.
X
BE
GF
ΜΖΑ
DE
MZD
N =
mZK
MZJ
MZH
GK
HL
ATHLAKGJ
3a+21,
H
K
(42)
3a
5a-7
J

Answer 1

x = 3

BE = 35

GF = 21

m∠A = 49°

DE = 18

m∠D = 95°

z = 8

m∠K = 32°

m∠J = 74°

m∠H = 74°

GK = 63

HL = 42

Explanation:

ΔAFG ≅ ΔEBD

If triangle AFG is congruent to triangle EBD then their corresponding side lengths are the same length:

• FA = BE
• GF = DB
• GA = DE

Therefore, we can create two equations using the given expressions for each side:

`FA=BE \implies 7y = 3y + 20`

`GA=DE\implies 3x + 9 = 8x - 6`

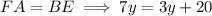
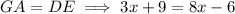
Solve the first equation for y:

`\begin{aligned}4y &= 20\\y &= 5\end{aligned}`

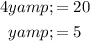
Therefore, the length of side BE is:

`BE = 3(5)+20`

`BE=15+20`

`BE=35`

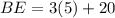
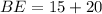
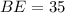
Solve the second equation for x:

`\begin{aligned}3x + 9 &= 8x - 6\\15& = 5x\\5x&=15\\x&=3\end{aligned}`

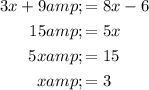
Therefore, the length of side DE is:

`DE = 8(3)-6`

`DE=24-6`

`DE=18`

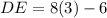
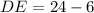
To find the length of side GF, substitute the value of x = 3 into the expression for side GF:

`GF=7(3)`

`GF= 21`

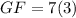
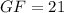
As triangle AFG is congruent to triangle EBD then their corresponding angles have the same measure:

• m∠A = m∠E
• m∠F = m∠B
• m∠G = m∠D

Given m∠G = 95°, then:

`m\angle D = 95^(\circ)`

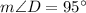
The interior angles of a triangle sum to 180°. Therefore, given m∠B = 36° and m∠D = 95° then:

`m \angle E = 180^(\circ) - 36^(\circ) - 95^(\circ)`

`m \angle E= 49^(\circ)`

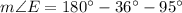
Finally, as m∠A = m∠E, then:

`m \angle A= 49^(\circ)`

`\hrulefill`

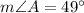
ΔIHL ≅ ΔKGJ

If triangle IHL is congruent to triangle KGJ then their corresponding side lengths are the same length:

• IH = KG
• HL = GJ
• IL = KJ

Both triangles are isosceles triangles since two of their interior angles are congruent. Therefore:

• IH = IL = KG = KJ

To find the value of a, we can create an equation using the given side expressions:

`KJ=IH\implies 5a-7=3a+21`

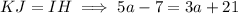
Solve the equation for a:

`\begin{aligned}5a-7&=3a+21\\2a&=28\\a&=14\end{aligned}`

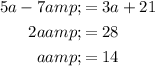
As GK = KJ, we can use the expression for side KJ to find the length of side GK. Substitute a = 14 into the expression:

`GK=5(14)-7`

`GK=70-7`

`GK=63`

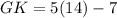
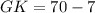
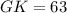
As HL = GJ, we can use the expression for side GJ to find the length of side HL:

`HL=3(14)`

`HL=42`

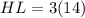
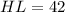
As triangle IHL is congruent to triangle KGJ then their corresponding angles have the same measure:

• m∠I = m∠K
• m∠H = m∠G
• m∠L = m∠J

Given m∠I = 32°, then:

`m\angle K = 32^(\circ)`

As the measure of K is (4z)°, then:

`(4z)^(\circ)=32^(\circ)`

`4z=32`

`z=8`

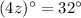
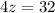
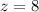
As triangles IHL and KGJ are isosceles, then their base angles are of equal measure:

• m∠H = m∠G = m∠L = m∠J

The interior angles of a triangle sum to 180°, so to find the measure of angles H, G, L and J, we can subtract the measure of angle I from 180°, and then divide the result by 2:

`m \angle H = (180^(\circ) - 32^(\circ))/(2)`

`m \angle H = (148^(\circ))/(2)`

`m \angle H = 74^(\circ)`

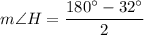
Finally, as m∠J = m∠H, then:

`m \angle J = 74^(\circ)`