Answer:
A) The price of fuel A is decreasing by 5 percent each month.
B) The price of fuel B is decreasing by 4 percent each month.
C) Fuel A
Explanation:
Part A
To calculate the percentage change for fuel A per month, we can use the provided Percentage Change Formula:
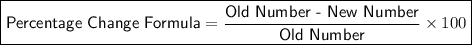
Calculate the percentage change between consecutive months by substituting the given values into the formula, and rounding to the nearest percent:
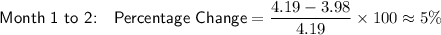
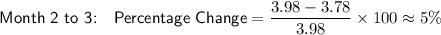
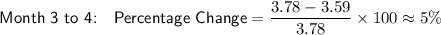
So, the price of fuel A is decreasing by approximately 5 percent each month.

Part B
The price f(x), in dollars, of fuel B after x months is represented by the function:

This is an exponential decay function, in the form f(x) = a(1 - r)ˣ, where "a" is the initial value and "r" is the percentage decrease in decimal form.
Therefore, to calculate the percentage decrease for fuel B, we can set (1 - r) equal to 0.96, and solve for r:


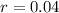
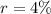
Therefore, the price of fuel B is decreasing by 4 percent each month.

Part C
Comparing the percentage changes, fuel A is decreasing by approximately 5% each month, while fuel B is decreasing by 4% each month. Therefore, fuel A recorded a greater percentage change.