Define an exponential function, h(x), which passes through the points (1,16) and
(5, 1296). Enter your answer in the form axb^x
the equation is of the form
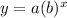
we have
point (1,16)
so
For x=1, y=16
substitute
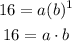
isolate the variable a
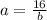
Point (5,1296)
For x=5, y=1,296
substitute
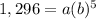
substitute equation 1 in equation 2
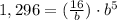
solve for b
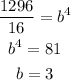
Find the value of a
a=16/3
therefore
the equation is
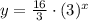
see the attached figure to better understand the problem