Question

Define an exponential function, h(x), which passes through the points (1,16) and(5, 1296). Enter your answer in the form axb^xh(x) =

Answer 1

Define an exponential function, h(x), which passes through the points (1,16) and

(5, 1296). Enter your answer in the form axb^x

the equation is of the form

`y=a(b)^x`

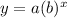
we have

point (1,16)

so

For x=1, y=16

substitute

`\begin{gathered} 16=a(b)^1 \\ 16=a\cdot b \end{gathered}`

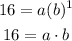
isolate the variable a

`a=(16)/(b)`

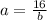
Point (5,1296)

For x=5, y=1,296

substitute

`1,296=a(b)^5`

substitute equation 1 in equation 2

`1,296=((16)/(b))\cdot b^5`

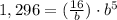
solve for b

`\begin{gathered} (1296)/(16)=b^4 \\ b^4=81 \\ b=3 \end{gathered}`

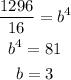
Find the value of a

a=16/3

therefore

the equation is

`y=(16)/(3)\cdot(3)^x`

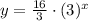
see the attached figure to better understand the problem