Question

Please help !!!!!

If f(x) = x + ln x for all values of x on the closed interval [1, 4], for what value of x is the instantaneous rate of change of y with respect to x the same as the average rate of change in the interval [1, 4]?

Answer 1

Answer: x = 2.164043 (approximate)

Step-by-step explanation

The average rate of change (AROC) formula is

`\text{AROC} = (f(b)-f(a))/(b-a)`

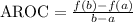
If you plugged in x = 1 you should get f(1) = 1

Also, f(4) = 4 + ln(4) = 5.386294 approximately.

So,

`\text{AROC} = (f(b)-f(a))/(b-a)\\\\\text{AROC} = (f(4)-f(1))/(4-1)\\\\\text{AROC} \approx (5.386294 - 1)/(4-1)\\\\\text{AROC} \approx (4.386294)/(3)\\\\\text{AROC} \approx 1.462098\\\\`

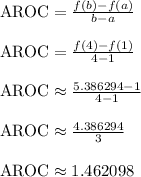
This is the approximate slope of the secant line through (1,1) and (4,5.386294). Notice the AROC formula is basically the slope formula.

We'll set this slope value equal to the derivative f ' (x) = 1 + (1/x) so we can solve for x. This will help us find when the tangent slope is equal to this value.

f ' (x) = 1.462098

1 + (1/x) = 1.462098

1/x = 1.462098 - 1

1/x = 0.462098

x = 1/0.462098

x = 2.164043

This is the approximate final answer. Round it however needed.