Question

I need to know the new equation, I’ve provided a picture

Answer 1

Hello there. To solve this question, we'll simply have to make x => x + 5 in the function.

Given the function:

`f(x)=4x^2-3^{}`

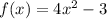
We have to determine f(x + 5)

By making x => x + 5 in this function, we get:

`f(x+5)=4\cdot(x+5)^2-3`

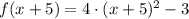
Now remember the binomial expansion of order 2:

`(a+b)^2=a^2+2ab+b^2`

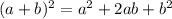
Therefore we have:

`f(x+5)=4\cdot(x^2+2\cdot x\cdot5+5^2)-3`

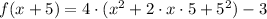
Multiply the terms inside parentheses and calculate the square.

`f(x+5)=4\cdot(x^2_{}+10x+25)-3`

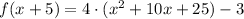
Apply the distributive property

`f(x+5)=4x^2+4\cdot10x+4\cdot25-3`

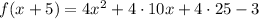
Multiply and add the numbers

`\begin{gathered} f(x+5)=4x^2+40x+100-3 \\ \boxed{f(x+5)=4x^2+40x+97} \end{gathered}`

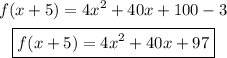
This is the answer we're looking for.

A way of showing this is the correct answer is to make x = 1 and x = 6 in the former function:

`\begin{gathered} f(1)=4\cdot1^2-3=4\cdot1-3=4-3=1 \\ f(6)=4\cdot6^2-3=4\cdot36-3=144-3=141 \end{gathered}`

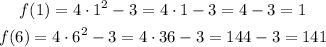
Then making x = 1 in the expression we found after:

`f(1+5)=f(6)=4\cdot1^2+40\cdot1+97=4+40+97=141`

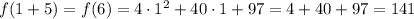
As expected.