Question

The cockroach population in a particular apartment building can be approximated by an exponential function, with a growth rate of 3.2% per month. After about how many months will the population double, to the nearest month?

Answer 1

22 months

Explanation:

To solve this problem, we can use the following formula for exponential growth:

`\boxed{\boxed{\sf A = P(1 + r)^t }}`

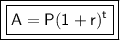
where:

• A is the final population
• P is the initial population
• r is the growth rate
• t is the time in years

Let the initial population is P = x cockroaches, the growth rate is r = 3.2% = 0.032 per month, and we want to find the time t in months when the population doubles, which means A = 2P = 2x cockroaches.

Substituting these values into the formula, we get:

`\sf 2x = x (1 + 0.032)^t`

`\sf 2 \cdot \cancel{x}=\cancel{x} ( 1.032)^t`

`\sf 2 = ( 1.032)^t`

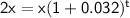
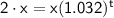
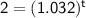
Taking the logarithm of both sides (in base 10), we get:

`\sf log(2) = t log(1.032)`

Dividing both sides by log(1.032), we get:

`\sf t =( log(2) )/( log(1.032))`

Evaluating this expression, we get:

`\sf t = 22.005603578508`

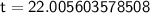
In nearest month

t = 22 months

Therefore, the cockroach population will double after about 22 months.