Question

You have two spinners each with three sections of equal size, one labeled with the numbers 1,2,3 and the others 2,4,6. You spin both and observe the numbers. Let X be the sum of the two numbers. In the game you are playing, you win if you get a sum of at least a 600 in 100 spins. If not you lose, should I play?

Answer 1

From the table

`\text{Total possible outcomes = 9}`

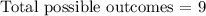
we are to find the probability of getting a sum of at least 600 in 100 spins

This means, we need to get a sum of at least 6 in 1 spin

Hence

`\begin{gathered} P(\text{getting a sum of at least }6\text{ in one spin)} \\ =\text{ }\frac{number\text{ of possible outcome}}{total\text{ possible outcome}} \end{gathered}`

From the table

number of the possible outcome of getting a sum of at least 6 = 5

Therefore

`\begin{gathered} P(\text{getting sum of at least 6 in one spin)} \\ =\text{ }(5)/(9) \\ \cong\text{ 0.56} \end{gathered}`

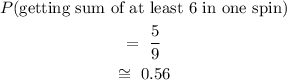
Since the probability is more than 0.5 then

I can play the game