From the table
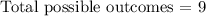
we are to find the probability of getting a sum of at least 600 in 100 spins
This means, we need to get a sum of at least 6 in 1 spin
Hence

From the table
number of the possible outcome of getting a sum of at least 6 = 5
Therefore
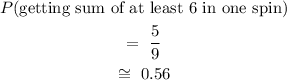
Since the probability is more than 0.5 then
I can play the game