Question

Find the angles look at the picture

Answer 1

• m∠B = 42°
• m∠E = 69°
• m∠ECD = 42°
• m∠ACD = 138°

Explanation:

Given;

• ∆ ABC is an isoceles triangle.
• ∆CDE is an isoceles triangle.
• m∠A = 96°

To find:

• m∠B = ?
• m∠E = ?
• m∠ECD = ?
• m∠ACD = ?

Solution:

Since the base angle of isoceles triangle are equal.

So,

m∠B = m∠C

We know that

Sum of interior angles of a triangle is equal to 180°.

So,

m∠A + m∠B + m∠C = 180°

Substitute known value

96° + m∠C + m∠C = 180°

96° + 2m∠C = 180°

2m∠C = 180° - 96°

2m∠C = 84°

`\sf m \angle C =(84^\circ)/(2)`

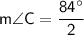
m∠C = 42°

Since m∠B = m∠C so,

m∠B = 42°

Similarly

Sum of interior angles of a triangle is equal to 180°.

so,

m∠CDE + m∠CED + m∠ECD = 180°

Here

∆ CDE is an isoceles triangle.

So, it's base angle are equal, which is:

m∠CDE = m∠CED

And

m∠C = m∠ECD = 42° Vertically Opposite Angle are equal.

Substitute these known value:

Here

m∠CED + m∠CED + 42° = 180°

2m∠CED + 42° = 180°

2m∠CED = 180° - 42°

2m∠CED = 138°

`\sf m\angle CED =(138^\circ)/(2)`

m∠CED = 69°

So,

m∠CDE = 69°

And finally

m∠ACD and m∠C are linear pair and they are supplementary.

So,

m∠ACD + m∠C = 180°

m∠ACD + 42° = 180°

m∠ACD = 180° - 42°

m∠ACD = 138°

Therefore, final answer is:

• m∠B = 42°
• m∠E = 69°
• m∠ECD = 42°
• m∠ACD = 138°