Question

27, 9, 3, 1, 1/3,1/9....What is the value of the 10th term in the sequence?

Answer 1

`27,9,3,1,(1)/(3),(1)/(9)`

1. Identify if the sequence has a common difference or a common ratio.

Common difference: subtract each term from the next term:

`\begin{gathered} 9-27=-18 \\ 3-9=-6 \\ 1-3=-2 \end{gathered}`

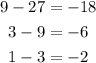
There is not a common difference.

Common ratio: Divide each term into the previous term:

`\begin{gathered} (9)/(27)=(1)/(3) \\ \\ (3)/(9)=(1)/(3) \\ \\ (1)/(3)=(1)/(3) \\ \\ ((1)/(3))/(1)=(1)/(3) \\ \\ ((1)/(9))/((1)/(3))=(3)/(9)=(1)/(3) \end{gathered}`

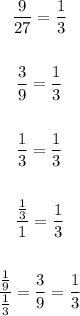
The common ratio is 1/3; it is a geometric sequence.

2. Use the next fromula to write the formula to find the nth term in the sequence:

`\begin{gathered} a_n=a_1*r^(n-1) \\ \\ r:common\text{ }ratio \end{gathered}`
`a_n=27*((1)/(3))^(n-1)`

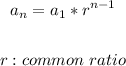
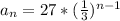
Evaluare the formula above for n=10 to find the 10th term:

`\begin{gathered} a_(10)=27*((1)/(3))^(10-1) \\ \\ a_(10)=27*((1)/(3))^9 \\ \\ a_(10)=27*(1)/(3^9) \\ \\ a_(10)=27*(1)/(19683) \\ \\ a_(10)=(27)/(19683) \\ \\ a_(10)=(1)/(729) \end{gathered}`

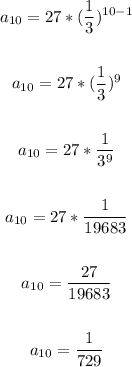
Then, the 10th term is 1/729