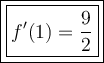Question

Attached below is my question. It is differential calculus. I greatly thank you for any help or time that you spend on this..! Have a most wonderful day!

Answer 1

`f'(x)=(9x^2+3x-3)/(2x√(x))`

`f'(1)=(9)/(2)`

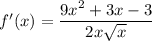
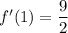
Explanation:

Given rational function:

`f(x)=(3x^2+3x+3)/(√(x))`

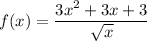
To find f'(x), we can differentiate the function f(x) using the quotient rule:

`\boxed{\begin{array}{c}\underline{\textsf{Quotient Rule for Differentiation}}\\\\\textsf{If $y=(u)/(v)$ then:}\\\\\frac{\text{d}y}{\text{d}x}=\frac{v \frac{\text{d}u}{\text{d}x}-u\frac{\text{d}v}{\text{d}x}}{v^2}\\\\\end{array}}`

First, identify u and v and differentiate them separately using the power rule and the constant rule:

`\boxed{\begin{array}{l}\underline{\textsf{Differentiation Rules}}\\\\\textsf{Power Rule:}\quad \frac{\text{d}}{\text{d}x}\left(ax^n\right)=n\cdot ax^(n-1)\\\\\textsf{Constant Rule:}\quad\frac{\text{d}}{\text{d}x}\left(a\right)=0\\\\\textsf{(where $a$ is a constant)}\end{array}}`

Therefore:

`\begin{aligned}u=3x^2+3x+3 \implies \frac{\text{d}u}{\text{d}x}&=2 \cdot 3x^(2-1)+1 \cdot 3x^(1-1)+0\\\\\frac{\text{d}u}{\text{d}x}&=6x^1+3x^0\\\\\frac{\text{d}u}{\text{d}x}&=6x+3(1)\\\\\frac{\text{d}u}{\text{d}x}&=6x+3\end{aligned}`

`\begin{aligned}v=√(x)=x^(\frac12) \implies \frac{\text{d}v}{\text{d}x}&=(1)/(2)\cdot x^(\frac12-1)\\\\\frac{\text{d}v}{\text{d}x}&=(1)/(2)x^(-\frac12)\\\\\frac{\text{d}v}{\text{d}x}&=(1)/(2x^(\frac12))\\\\\frac{\text{d}v}{\text{d}x}&=(1)/(2√(x))\end{aligned}`

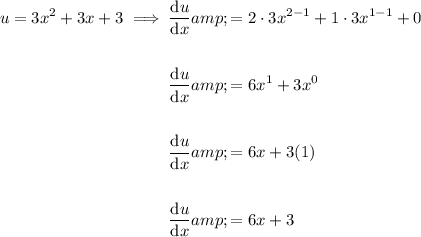
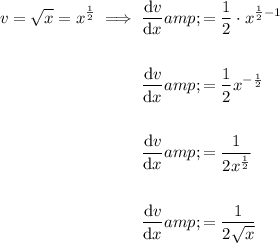
Now, substitute everything into the quotient rule:

`\frac{\text{d}y}{\text{d}x}=(√(x) \cdot (6x+3)-(3x^2+3x+3)\cdot (1)/(2√(x)))/(\left(√(x)\right)^2)`

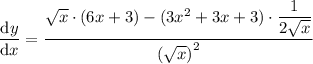
Simplify:

`\frac{\text{d}y}{\text{d}x}=(√(x) \cdot (6x+3)-(3x^2+3x+3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=((2√(x)√(x) (6x+3))/(2√(x))-(3x^2+3x+3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=((2x(6x+3))/(2√(x))-(3x^2+3x+3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=((12x^2+6x)/(2√(x))-(3x^2+3x+3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=((12x^2+6x-3x^2-3x-3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=((9x^2+3x-3)/(2√(x)))/(x)`

`\frac{\text{d}y}{\text{d}x}=(9x^2+3x-3)/(2x√(x))`

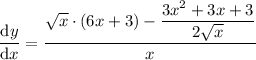
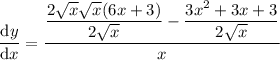
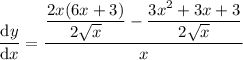
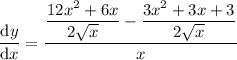
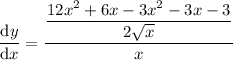
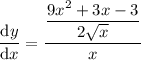
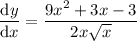
Therefore, the derivative of function f(x) is:

`\large\boxed{\boxed{f'(x)=(9x^2+3x-3)/(2x√(x))}}`

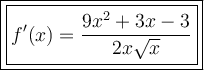
To find f'(1), simply substitute x = 1 into f'(x):

`f'(1)=(9(1)^2+3(1)-3)/(2(1)√(1))`

`f'(1)=(9(1)+3(1)-3)/(2(1)(1))`

`f'(1)=(9+3-3)/(2)`

`f'(1)=(9)/(2)`

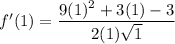
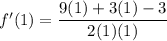
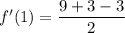
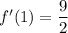
Therefore, the value of f'(1) is:

`\large\boxed{\boxed{f'(1)=(9)/(2)}}`

Answer 2

`\displaystyle f'(x)=(9x^2+3x-3)/(2x^(3)/(2))`

`\displaystyle f'(1)=(9)/(2)`

Explanation:

We can use the power rule and the quotient rule to find f'(x) and f'(1). Let us review how to apply these derivative rules.

`\displaystyle \boxed{\text{Power Rule: } (d)/(dx)(x^n)=n*x }`

`\displaystyle \boxed{\text{Quotient Rule:}\;\;\frac{d}{{dx}}\left( {\frac{{f\left( x \right)}}{{g\left( x \right)}}} \right) = \frac{{\frac{d}{{dx}}f\left( x \right)g\left( x \right) - f\left( x \right)\frac{d}{{dx}}g\left( x \right)}}{{g^2 \left( x \right)}}}`

Now we can find the derivative. Take the derivative of both sides of the equation.

➜ Take note that
`√(x) =x^(1)/(2)`.

`\displaystyle f'(x)=\frac{x^(1)/(2) (6x+3)-(3x^2+3x+3)((1)/(2)x^{-(1)/(2)} )}{(√(x) )^2}}`

Next, we can simplify this a little bit.

Square.

`\displaystyle f'(x)=\frac{x^(1)/(2) (6x+3)-(3x^2+3x+3)((1)/(2)x^{-(1)/(2)} )}{x}`

Distribute.

`\displaystyle f'(x)=\frac{6x^(3)/(2)+3x^(1)/(2)-((3)/(2)x^(3)/(2)+(3)/(2)x^(1)/(2)+(3)/(2)x^{-(1)/(2)} )}{x}`

`\displaystyle f'(x)=\frac{6x^(3)/(2)+3x^(1)/(2)-(3)/(2)x^(3)/(2)-(3)/(2)x^(1)/(2)-(3)/(2)x^{-(1)/(2)}}{x}`

Combine like terms and simplify.

➜ Take note that a negative exponent becomes positive when moved to the denominator.

`\displaystyle f'(x)=(9x^2+3x-3)/(2x^(3)/(2))`

Lastly, we will substitute 1 for x to find f'(1).

`\displaystyle f'(x)=(9x^2+3x-3)/(2x^(3)/(2))`

`\displaystyle f'(1)=(9(1)^2+3(1)-3)/(2(1)^(3)/(2))`

Simplify:

`\displaystyle f'(1)=(9+3-3)/(2)`

`\displaystyle f'(1)=(9)/(2)`