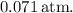Question

A reaction between liquid reactants takes place at -13.0 C in a sealed, evacuated vessel with a measured volume of 35.0L. . Measurements show that the reaction produced 17. g of sulfur hexafluoride gas. Calculate the pressure of sulfur hexafluoride gas in the reaction vessel after the reaction

Answer 1

The pressure of sulfur hexafluoride gas in the reaction vessel after the reaction is approximately
`\(0.071 \, \text{atm}\).`

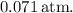
To calculate the pressure of sulfur hexafluoride gas in the reaction vessel, we can use the ideal gas law formula:

PV = nRT

Where:

- P is the pressure we want to find.

- V is the volume of the vessel, which is 35.0 L.

- n is the number of moles of the sulfur hexafluoride gas.

- R is the ideal gas constant,

- T is the temperature, which needs to be in Kelvin.

First, we convert the temperature from Celsius to Kelvin:

`\[ T (\text{K}) = T (\text{°C}) + 273.15 \]`

`\[ T = -13.0 + 273.15 \]`

Next, we calculate the number of moles of sulfur hexafluoride (SF6). The molar mass of SF6 is the sum of the atomic masses of sulfur (32.07 g/mol) and six fluorine atoms (6 × 19.00 g/mol).

`\[ \text{Molar mass of SF6} = 32.07 + 6 * 19.00 \]`

Then we find the number of moles:

`\[ n = \frac{\text{mass}}{\text{molar mass}} \]`

`\[ n = \frac{17.0 \, \text{g}}{\text{Molar mass of SF6}} \]`

Finally, we rearrange the ideal gas law to solve for P :

`\[ P = (nRT)/(V) \]`

Let's calculate these values step by step.

The pressure of sulfur hexafluoride gas in the reaction vessel after the reaction is approximately
`\(0.071 \, \text{atm}\).`

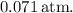
Here's the step-by-step calculation:

1. Temperature Conversion to Kelvin:

`\[ T = -13.0 + 273.15 = 260.15 \, \text{K} \]`

2. Calculate Molar Mass of SF6:

`\[ \text{Molar mass of SF6} = 32.07 + 6 * 19.00 = 146.07 \, \text{g/mol} \]`

3. Calculate Moles of SF6:

`\[ n = \frac{17.0 \, \text{g}}{146.07 \, \text{g/mol}} \]`

4. Calculate Pressure using Ideal Gas Law:

`\[ P = (nRT)/(V) \]`

Using the values, we find the pressure to be approximately
`\(0.071 \, \text{atm}\).`