Answer:

Explanation:
To factor the cubic polynomial
 , we can use various methods.
, we can use various methods.
In this case, I'll use synthetic division to find one factor and then factorize the quadratic remaining.
1. First, we can try to find a root by testing potential factors of the constant term (36) divided by potential factors of the leading coefficient (1).
Let's try
 because it often makes calculations easier.
because it often makes calculations easier.
Synthetic Division:
![\sf \begin{array}c -1 & 1 & 10 & 33 & 36 \\ & \downarrow & -1 & -9 & -24 \\ \hline & 1 & 9 & 24 & 12 \\\end{array}]()
The remainder is 12, not 0.
So,
 is not a root.
is not a root.
2. Next, let's try
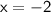 :
:
![\sf \begin{array}c -2 & 1 & 10 & 33 & 36 \\ & \downarrow & -2 & -16 & 6 \\ \hline & 1 & 8 & 17 & 42 \\ \end{array}]()
Again, the remainder is not 0.
3. Let's try
 :
:
![\sf \begin{array}c -3 & 1 & 10 & 33 & 36 \\ & \downarrow & -3 & -21 & -36 \\ \hline & 1 & 7 & 12 & 0 \\ \end{array}]()
We find that
 is a root because the remainder is 0.
is a root because the remainder is 0.
4. Now, we can factor the polynomial as
 .
.
5. Further factor the quadratic term
 by factoring it into:
by factoring it into:




 .
.
So, the completely factored form of
 is
is
 .
.