Question

Mass of 3.1 kg is moving with a speed of 5.9 m/s upward. later on during its flight, the mass is moving at 7.8 m/ downward. ignore air resistance. what is the change in the potential energy of the mass/earth system between the moments described?

Answer 1

Approximately
`40\; {\rm J}` lower than the initial value.

Step-by-step explanation:

The mechanical energy of a system is equal to the sum of its kinetic energy (
`\text{KE}`) and its potential energy (
`\text{PE}`). Under the assumptions, the total mechanical energy of this system should be conserved. In other words, the total change in kinetic energy and the change in potential energy, combined, should be zero:

`\displaystyle (\text{change in KE}) + (\text{change in PE}) = 0`.

Rearrange this equation to find the change in potential energy (
`\text{PE}`):

`(\text{change in PE}) = - (\text{change in KE})`.

When an object of mass
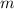`m` is travelling at a speed of
`v`, the kinetic energy of this object would be
`(1/2)\, m\, v^(2)`. Note that the kinetic energy of the object depends only on the magnitude of velocity and not on the direction of the motion. For example, the kinetic energy of an object travelling upward at
`v = 7.8\; {\rm m\cdot s^(-1)}` is the same as the kinetic energy of the same object travelling downward at the same speed.

Let
`u = 5.9\; {\rm m\cdot s^(-1)}` denote the original speed of this object, and let
`v = 7.8\; {\rm m\cdot s^(-1)}` denote the new speed of the object. The mass of this object is
`m = 3.1\; {\rm kg}`. As the speed of this object changed from
`u` to
`v`, the change in the kinetic energy of this object would be:

`\begin{aligned}(\text{change in KE}) &= (\text{final KE}) - (\text{initial KE}) \\ &= (1)/(2)\, m\, v^(2) - (1)/(2)\, m\, u^(2) \\ &= (1)/(2)\, m\, (v^(2) - u^(2))\end{aligned}`.

Since
`(\text{change in PE}) = - (\text{change in KE})`, the change in the potential energy of this object would be:

`\begin{aligned}(\text{change in PE})&= -(\text{change in KE}) \\ &= -(1)/(2)\, m\, (v^(2) - u^(2)) \\ &= (1)/(2)\, m\, (u^(2) - v^(2)) \\ &= (1)/(2)\, (3.1)\, (5.9^(2) - 7.8^(2)) \; {\rm J} \\ &\approx (-40)\; {\rm J}\end{aligned}`.

Note that the change in potential energy is negative, meaning that the new value of the potential energy is lower than the initial value.

In other words, the new value of the potential energy of this object would be approximately
`40\; {\rm J}` lower than the initial value.