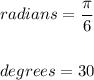EXPLANATIONS:
Given;
We are given the following expression;
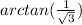
Required;
We are required to find the angle measure of this in both radians, and degrees.
Step-by-step solution;
For the angle whose tangent is given as 1 over square root of 3, on the unit circle, we would have
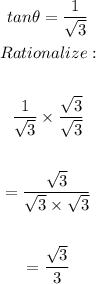
On the unit circle, the general solution for this value as shown would be;
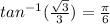
To convert this to degree measure, we will use the following equation;
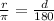
We now substitute for the value of r;

We now cross multiply;
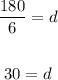
Therefore;
ANSWER: