Question

The graph below shows a company’s profit f(x) in dollars, depending on the price of goods x, in dollar’s, being sold by the company: Part A: What do the x-intercepts and maximum value of the graph represent in context of the disrobed situation?Part B: What are the intervals where the function is increasing and decreasing, and what do they represent about the sale and profit for the company in the situation described?Part C: What is an approximate average rate of change of the graph from x=1 to x=3, and what does this rate represent in context of the described situation?

Answer 1

We will have the following:

Part A:

The x-intercepts represent the prices of the goods than wen sold represent no net gain or loss.

The maximum value represents the price at which there will be a maximum profit.

Part B:

We will have that the increasing and decreasing intervals are respectively:

`I_{\text{increaing}}=(-\, \infty,3)`
`I_{\text{decreasing}}=(3,\infty)`

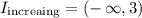
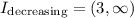
They tells us respectively that:

Increasing: The greater the price the greater the profit.

Decreasing: The greater the price the smaller the profit.

Part C:

We determine the equation of the parabola. We can see that it's vertex is located at (3, 120), we can also see that the parabola passes by the origin (0, 0); so:

`f(x)=a(x-3)^2+120\Rightarrow0=a(0-3)^2+120`
`\Rightarrow0=9a+120\Rightarrow9a=-120\Rightarrow a=-(40)/(3)`

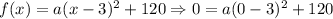
So, the equation that represents the parabola is:

`f(x)=-(40)/(3)(x-3)^2+120`

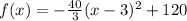
Then, we will determine the average rate of change as follows:

`\text{average rate of change}=(f(b)-f(a))/(b-a)`

So:

`\text{average rate of change}=((-40/3((3)-3)^2+120)-(-40/3((1)-3)^2+120))/(3-1)`
`\text{average rate of change}=(80)/(3)\Rightarrow average\text{ rate of change}\approx26.67`

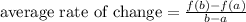
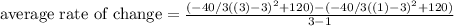
So, the avereage rate of change for the graph from x = 1 to x = 3 is exactly 80/3, that is approximately 26.67.