Question

Find the sector area for the angle of 7pi/6 on a circle with a radius of 6cm

Answer 1

In order to calculate the sector area, we can use the following rule of three, knowing that an angle of 2pi (complete circle) has an area of pi*r² (area of the circle).

So we have:

`\begin{gathered} \text{angle}\to\text{sector area} \\ 2\pi\to\pi r^2 \\ (7\pi)/(6)\to x \end{gathered}`

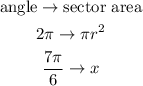
Now, we can write the following proportion and solve the equation for x:

`\begin{gathered} (2\pi)/((7\pi)/(6))=\frac{\pi r^2^{}}{x}^{} \\ x\cdot2\pi=(7\pi)/(6)\cdot\pi r^2 \\ x=((7\pi)/(6)\cdot\pi r^2)/(2\pi) \\ x=(7)/(12)\pi r^2 \\ x=(7)/(12)\pi\cdot6^2 \\ x=(7)/(12)\pi\cdot36 \\ x=21\pi\text{ cm}^2 \end{gathered}`

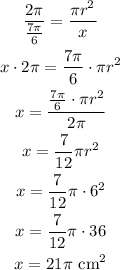
Therefore the sector area is 21pi cm².