Question

Attached below is the image for my question. It is differential calculus. If you take the time to help me, know that I greatly appreciate it. Thank you.

Answer 1

`f'(-1)=17`

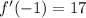
Explanation:

Given function:

`f(x) = x^5\:h(x)`

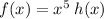
To calculate f'(-1), we first need to differentiate function f(x).

To do this, we can use the product rule.

`\boxed{\begin{array}{c}\underline{\sf Product\;Rule\;for\;Differentiation}\\\\\textsf{If}\;y=uv\;\textsf{then:}\\\\\frac{\text{d}y}{\text{d}x}=u\frac{\text{d}v}{\text{d}x}+v\frac{\text{d}u}{\text{d}x}\\\\\end{array}}`

First, identify u and v, and differentiate them separately with respect to x using the power rule of differentiation:

`\boxed{\begin{array}{c}\underline{\textsf{Power Rule of Differentiation}}\\\\ \frac{\text{d}}{\text{d}x}\left(x^n\right)=n\cdot x^(n-1)\\\\\end{array}}`

Therefore:

`\begin{aligned}u=x^5 \implies \frac{\text{d}u}{\text{d}x}&=5 \cdot x^(5-1)\\\\ \frac{\text{d}u}{\text{d}x}&=5x^(4)\end{aligned}`

`v=h(x) \implies \frac{\text{d}v}{\text{d}x}=h'(x)`

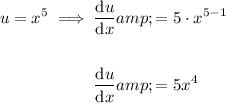
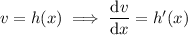
Now, substitute everything into the product rule:

`\frac{\text{d}y}{\text{d}x}=x^5 \cdot h'(x)+h(x) \cdot 5x^4`

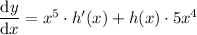
Therefore:

`f'(x)=x^5 \cdot h'(x)+h(x) \cdot 5x^4`

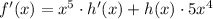
To calculate f'(-1), we can substitute x = -1, h(-1) = 5 and h'(-1) = 8 into the equation for f'(x):

`f'(-1)=(-1)^5 \cdot h'(-1)+h(-1) \cdot 5(-1)^4`

`f'(-1)=(-1) \cdot 8+5 \cdot 5(1)`

`f'(-1)=-8+5(5)`

`f'(-1)=-8+25`

`f'(-1)=17`

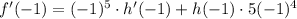
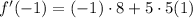
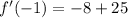
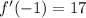
Therefore, the value of f'(-1) is:

`\large\boxed{\boxed{f'(-1)=17}}`

Answer 2

Answer: f'(-1) =17

Explanation:

It is given to us to use the product rule and the power rule. Let us first revisit what these rules are and how to apply them.

`\displaystyle \boxed{\text{Product Rule: }\\\frac{d}{{dx}}\left( {f\left( x \right)g\left( x \right)} \right) = f\left( x \right)\frac{d}{{dx}}g\left( x \right) + \frac{d}{{dx}}f\left( x \right)g\left( x \right)}`
`\displaystyle \boxed{\text{Power Rule: } (d)/(dx)(x^n)=n*x }`

Now, we will find the derivative of f(x).

Given:

`\displaystyle f(x) = x^5h(x)`

Take the derivative of both sides:

`\displaystyle f'(x) = (x^5)(h'(x)))+(h(x))(5x^4)`

Substitute known values to solve for f'(-1):

`\displaystyle f'(-1) = ((-1)^5)(h'(1)))+(h(1))(5(-1)^4)`

Simplify each term:

`\displaystyle f'(-1) = (-1)(8)+(5)(5)`

Multiply:

`\displaystyle f'(-1) =-8+25`

Add:

`\displaystyle f'(-1) =17`