Answer: the pressure of the gas in the container is approximately 0.529 atm.
Step-by-step explanation:
To calculate the pressure of
 molecules of
molecules of
 in a 21.0 L container at 273 K, we can use the Ideal Gas Law, which is given by:
in a 21.0 L container at 273 K, we can use the Ideal Gas Law, which is given by:
![\[ PV = nRT \]](https://img.qammunity.org/2024/formulas/chemistry/college/a99uftpldttp3mar5rusl3q2cnjbrkvv83.png)
Where:
 = pressure in atmospheres (atm)
= pressure in atmospheres (atm)
 = volume in liters (L)
= volume in liters (L)
 = number of moles of the gas
= number of moles of the gas
 = ideal gas constant
= ideal gas constant
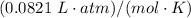
 = temperature in Kelvin (K)
= temperature in Kelvin (K)
First, we need to convert the number of molecules to moles using Avogadro's number
 :
:
![\[ n = \frac{3.0 * 10^(23) \ \text{molecules}}{6.022 * 10^(23) \ \text{molecules/mol}} \]](https://img.qammunity.org/2024/formulas/chemistry/college/jx126k354kvr0n4rwqq3jmqrbs9gvw5ps6.png)
![\[ n \approx 0.498 \ \text{moles} \]](https://img.qammunity.org/2024/formulas/chemistry/college/gsptn94dyvc8hy0po5ebzyut6l7wmc2vpc.png)
Now we can plug the values into the Ideal Gas Law and solve for pressure
 :
:
![\[ P = (nRT)/(V) \]](https://img.qammunity.org/2024/formulas/chemistry/college/26ok1pzonmty7h1vp6rie559t6jzhnu33g.png)
![\[ P = \frac{(0.498 \ \text{moles})(0.0821 \ L \cdot atm \cdot mol^(-1) \cdot K^(-1))(273 \ K)}{21.0 \ L} \]](https://img.qammunity.org/2024/formulas/chemistry/college/lhak58a3somulogd20w4lh2jiubcmzeck3.png)
![\[ P = ((0.498)(0.0821)(273))/(21.0) \]](https://img.qammunity.org/2024/formulas/chemistry/college/krheg4u294om37f7ewwhvk19etk8r4arha.png)
![\[ P \approx (11.104)/(21.0) \]](https://img.qammunity.org/2024/formulas/chemistry/college/86wg8oncc1a6egi9vax3oc4o4uh6g42zc5.png)
![\[ P \approx 0.52876 \ \text{atm} \]](https://img.qammunity.org/2024/formulas/chemistry/college/jniug8ygi5ie5q5rympxmzygi9vomtkwgr.png)