Question

The test scores on a 100-point test were recorded for 20 students:71 93 91 86 7573 86 82 76 5784 89 67 62 7277 68 65 75 84a. Can you reasonably assume that these test scores have been selected from a normal population? Use a stem and leaf plot to justify your answer.b. Calculate the mean and standard deviation of the scores.c. If these students can be considered a random sample from the population of all students, find a 95% confidence interval for the average test score in he population.

Answer 1

Answer: a. Yes

b. mean = 76.65

standard deviation = 10.04

c. 76.65 ± 4.4

Explanation:

a. Stem and leaf Plot shows the frequencies with which classes of value occur. To create this plot, we divide the set of numbers into 2 columns: stem, the left column, which contains the tens digits; leaf, the right column, which contains the unit digits.

Normal distribution is a type of distribution: it's a bell-shaped, symmetrical, unimodal distribution.

A stem and leaf plot displays the main features of the distribution. If turned on its side, we can see the shape of the data.

The figure below shows the stem and leaf plot of the 100-point test score. As we can see, when turned, the plot resembles bell-shaped distribution. So, this test scores were selected from a normal population.

b. Mean is the average number of a data set. It is calculated as the sum of all the data divided by the quantity the sample has:

mean =
`(\Sigma x)/(n)`

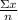
For the 100-point test score:

mean =
`(71+93+91+...+65+75+84)/(20)`

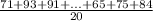
mean = 76.65

Standard Deviation determines how much the data is dispersed from the mean. It is calculated as:

`s=\sqrt{(\Sigma (x-mean)^(2))/(n-1) }`

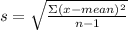
For the 100-point test score:

`s=\sqrt{([(71-76.65)+(93-76.65)+...+(84-76.65)]^(2))/(20-1) }`

s = 10.04

The mean and standard deviation of the scores are 76.65 and 10.04, respectively.

c. Confidence Interval is a range of values we are confident the real mean lies.

The calculations for the confidence interval is

mean ±
`z(s)/(√(n) )`

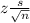
where

z is the z-score for the 95% confidence interval, which is equal 1.96

Calculating interval

76.65 ±
`1.96.(10.04)/(√(20) )`

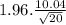
76.65 ± 4.4

The 95% confidence interval for the average test score in the population of students is between 72.25 and 81.05.